RC Passive and Active Filters Explained

In this post we are going to learn about RC (resistive and capacitive) frequency filters and we will be simulating each of the discussed frequency filters using proteus software.

We will be exploring the following frequency filters:

• Passive low pass filter.
• Passive high pass filter.
• Passive band pass filter.
• Active low pass filter.
• Active high pass filter.
• Active band pass filter.

Before we dive in to the above mentioned frequency filters, we will be exploring a fundamental concept called “capacitive reactance” of a capacitor. Capacitor is one of the key components which make RC frequency filters possible.

What is capacitive reactance of a capacitor?

To understand what capacitive reactance is, let’s consider a capacitor that is being charged on a DC voltage (say 9V); the capacitor starts to charge by drawing a charging current from the source and stops charging when the capacitor reaches exactly 9V. 

Now assume the source voltage is reduced to 6V, can you guess what will happen to the capacitor charged to 9V a few moments ago? The capacitor will discharge from 9V to 6V and stays at 6V. 

Now let’s assume the capacitor is connected to an AC supply (say 50 Hz sine wave), since the source’s voltage is changing its polarity 50 times a second, the capacitor is either charging or discharging at any given moment, also there is a flow of current through the capacitor at any given moment. 

When the current flows through the capacitor, the current flow faces some internal resistance or impedance, this internal impedance of a capacitor is called “capacitive reactance” measured in ohm (and its symbol is Xc). 

But, the internal impedance is not constant like a resistor but it is depended on the applied frequency.  

A capacitor behaves like this on an AC voltage supply:

• When the applied frequency increases the capacitive reactance decreases, meaning when the applied frequency is increased the internal impedance decreases. At very high frequencies a capacitor acts like a short circuit.
• When the applied frequency decreases the capacitive reactance increases, meaning when the applied frequency is decreased the internal impedance increases. At low frequencies or at 0 Hz a capacitor acts like open circuit. 

The following can be concluded from the above two statements:

1. A capacitor is a frequency depended component in an electric circuit. 
2. The capacitive reactance of a capacitor is inversely proportional to applied frequency.
3. At a higher frequency a capacitor acts like short-circuit and at a low frequency or at 0 Hz the capacitor acts like open circuit.

Capacitive reactance mathematically is given by: 

Xc (ohm) = 1/ 2π x f x C

Where, “Xc” is capacitive reactance in ohms.

              “f” is the applied frequency in Hz.

              “C” is the capacitance of the capacitor in farad. 

By now, you may have an idea what capacitive reactance is. 

Are frequency filters essentially potential dividers?  

Short answer is yes!

The RC filters consists of a resistor and a capacitor connected in series making it a voltage divider at the output node, one of the components is frequency depended i.e. capacitor whose impedance changes with frequency and the other component is frequency independent i.e. resistor. 

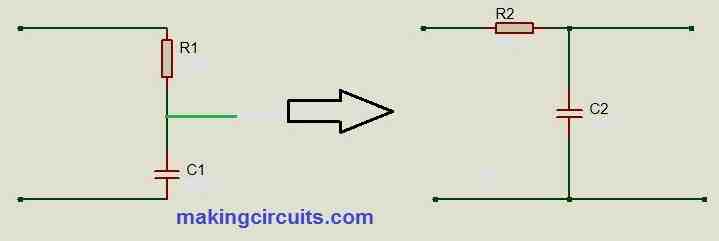
The RC circuit on the left hand side which resembles like a potential divider (actually it is) is rearranged on the right hand side. The rearranged circuit is what we frequently see on text books and on internet because it is easier cascade and connect with other circuits.

Passive Low Pass Filter:

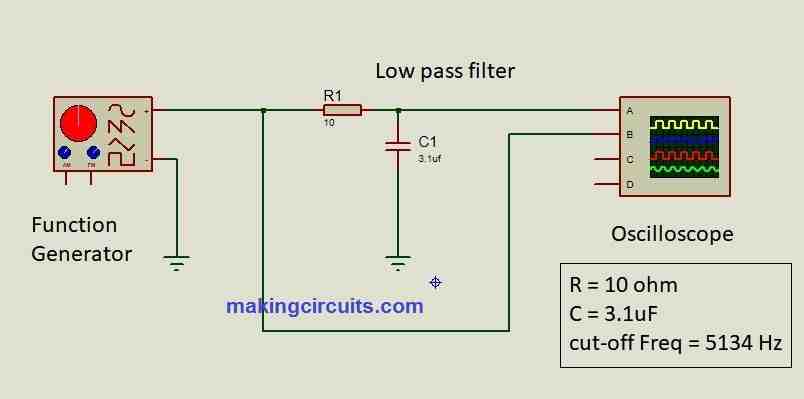
A passive low pass filter consists of passive components like resistor and capacitor and no semiconductors, hence the prefix “passive”. 

A low pass filter only allows lower frequencies to pass through the circuit and higher frequencies are blocked or attenuated. A low pass filter will allow frequencies from 0 Hz to a cut-off frequency.

The cut-off frequency of low pass filter can be calculated by using the below formula:

Fc = 1 / 2π x R x C

Where Fc is the cut-off frequency (-3dB),

             R is value of resistor in ohm,

             C is value of capacitor in farad.

You can also rearrange the above formula to find the values of resistor or capacitor for a given frequency. 

Now let’s assume R = 10 ohm and C = 3.1uF and by applying the values in the formula we get:

Fc = 1 / 2π x 10 x 3.1 x 10^-6

Fc = 5134.03 Hz or 5 KHz.

This low pass filter starts to attenuate the output if the applied frequency exceed above approx. 5 KHz.

Simulation of Low Pass Filter, cut-off at 5 KHz: Blue – input frequency, Yellow output frequency.

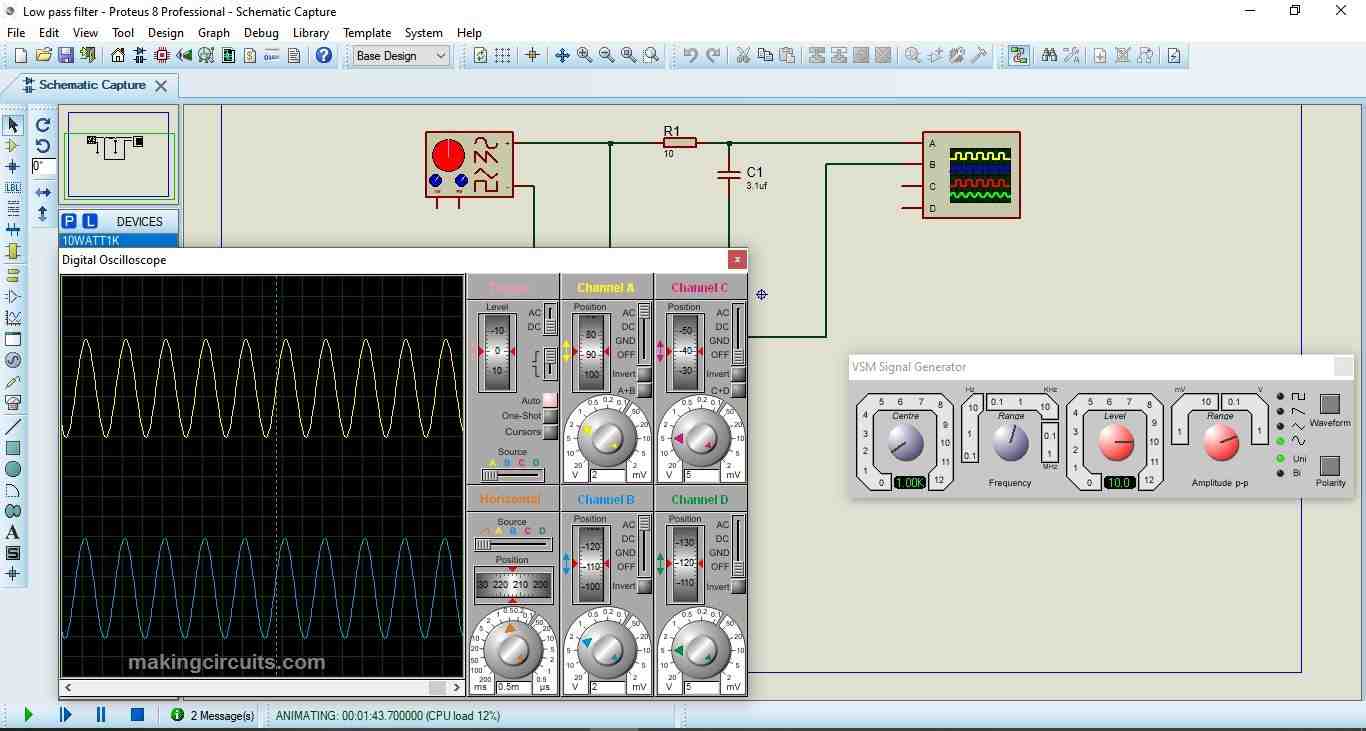
1 KHz: At 1 KHz we can observe that output is has negligible attenuation.   

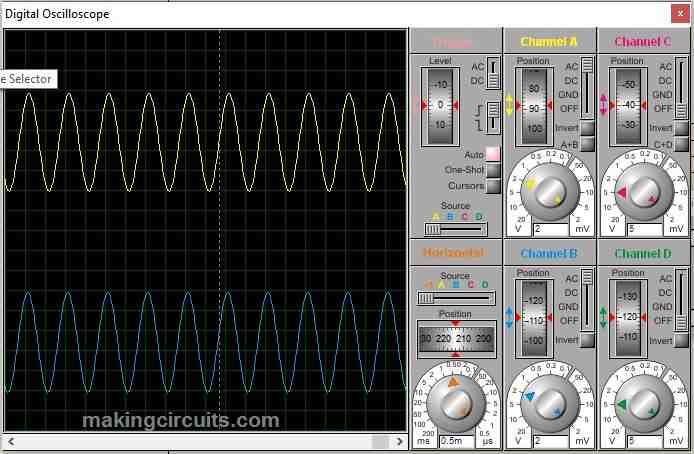
5 KHz: At cut-off frequency we can see attenuation has begun, the output amplitude is slightly small than the input.

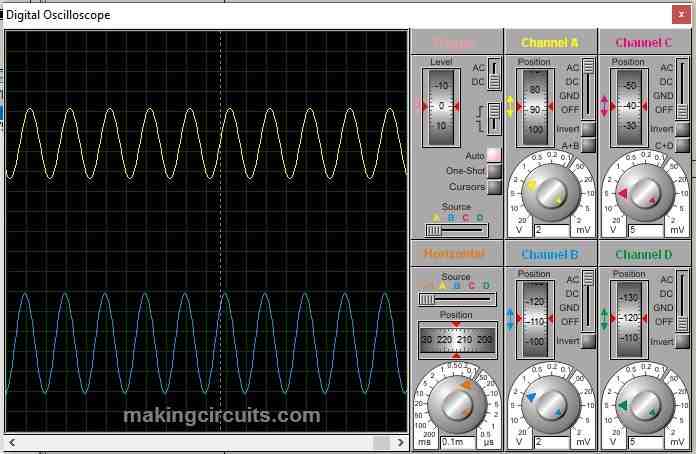
15 KHz: At 15 KHz we can see that the output has been attenuated to a great degree.

Typical low pass filter frequency response:

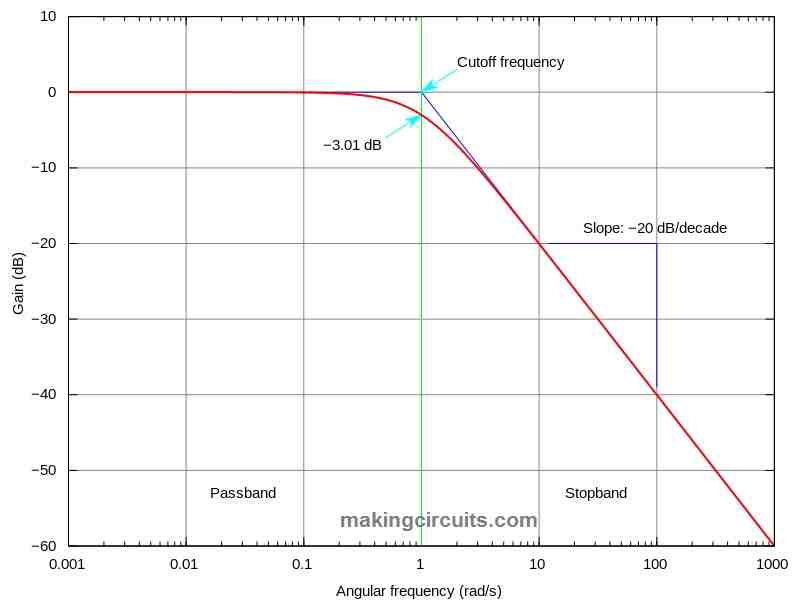
From the above frequency response graph we can infer that frequencies below a cut-off frequency are unaltered but frequencies past the cut-off frequency are attenuated. Higher the frequency input, higher the attenuation and vice-versa.

NOTE: RC low pass filter is also known as integrator circuit. 

Passive High Pass Filter:

High pass filter does the reverse operation of low pass filter. A high pass filter attenuates or blocks low frequencies and allows high frequencies to pass through the filter circuit (past cut-off frequency). This is achieved by rearranging the resistor and capacitor as illustrated below:

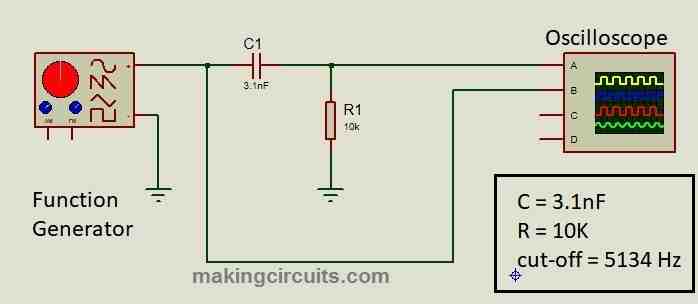
The cut-off frequency of high pass filter can be calculated by using the shown formula:

Fc = 1 / 2π x R x C

Where Fc is the cut-off frequency (-3 dB),

             R is value of resistor in ohm,

             C is value of capacitor in farad.

Now let’s assume R = 10K ohm and C = 3.1uF and by applying the values in the formula we get:

Fc = 1 / 2π x 10000 x 3.1 x 10^-9

Fc = 5134.03 Hz or 5 KHz.

The above shown circuit has a cut-off frequency of 5 KHz. Now let’s simulate the circuit and the output attenuates from 0 Hz to 5 KHz.

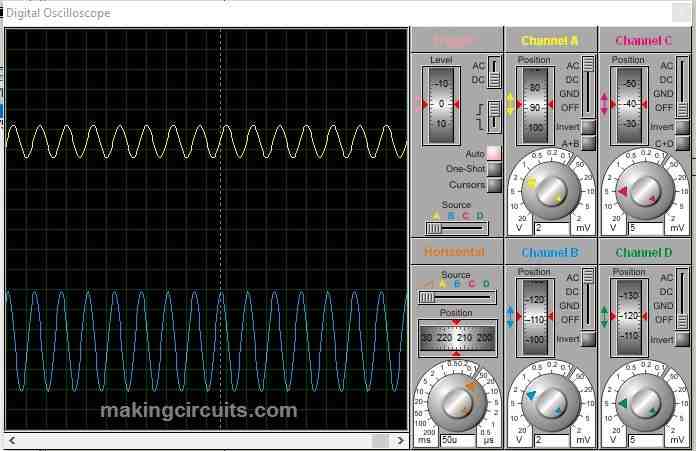
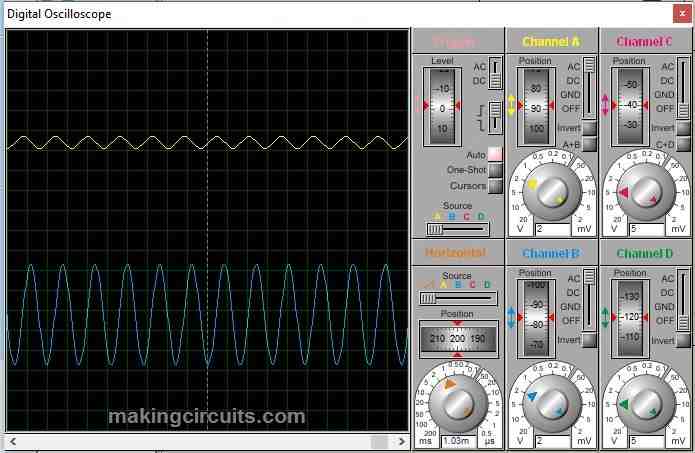
Simulation of passive high pass filter, cut-off 5 KHz: Blue – input frequency, Yellow output frequency.

At 600 Hz: At 600 Hz the output is significantly attenuated.

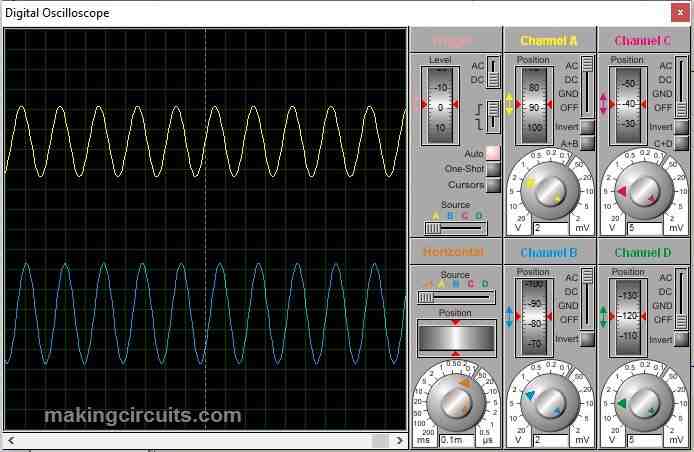
At 5 KHz: At 5 KHz or at cut-off frequency we can see the output has gained its amplitude significantly. 

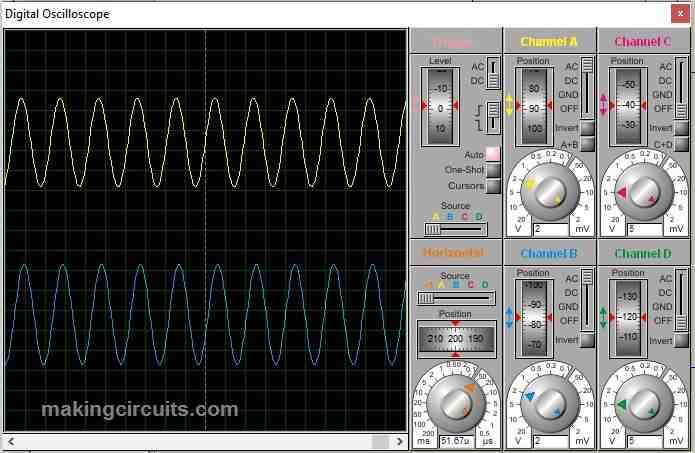
At 10 KHz: At 10 KHz we can observe that the output has negligible attenuation.

Typical low pass filter frequency response:

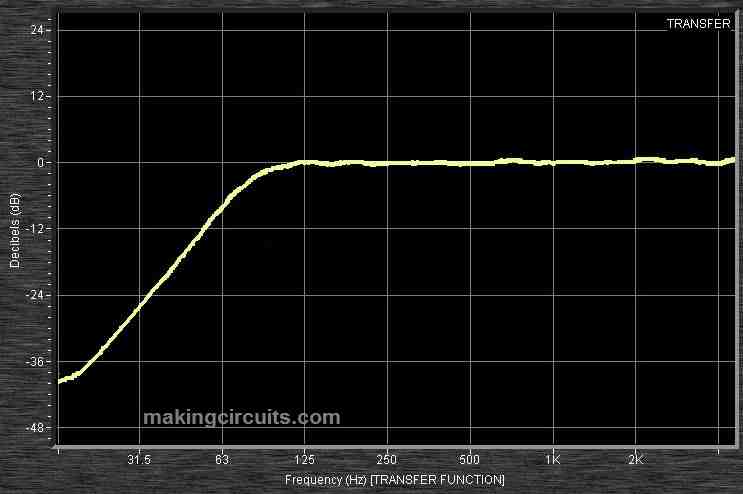
From the above graph we can infer that below the cut-off frequency the output is attenuated greatly and past the cut-off frequency the output is unaltered. Higher the input frequency, lower the attenuation and vice-versa.

NOTE: RC high pass filters are known as differentiator circuit. 

What is 2^nd order RC filter?

Before we dive into the next type of passive RC filter, we need to take a brief look at 2^nd order RC filters, only then you may be able to grasp the next section well.

The RC filters we have learned till now are called 1^st order RC filters. They got only one stage of filtration, if we add one more stage to the circuit, the RC filter can be said as 2^nd order RC filter.

2^nd order passive low pass filter:

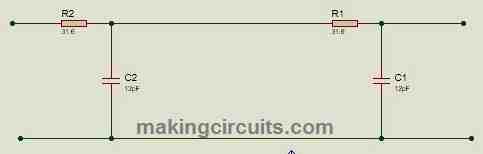
2^nd order passive high pass filter:

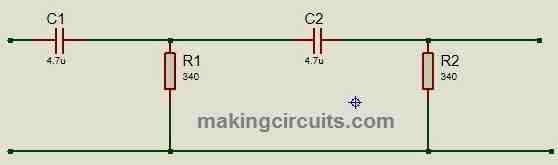
The advantage of 2^nd order filter is, they produce steeper cut-off slopes and gets steeper as we add more stages (higher order filters) and their disadvantage is the output amplitude gets feeble as we add more stages. 

NOTE: Formulas for calculating cut-off frequency for 2^nd order and higher orders are different from the 1^st order filters.

Passive band pass filter:

RC band pass filters are the kind of frequency filter which only allows a band of frequency to pass through and attenuates rest of the frequencies. Band pass filters are very useful in audio crossover filters where only a band or a range of frequencies are passed to tweeter, mid-range drivers, woofers and sub-woofers. 

For example: woofer and subwoofer produce bass (i.e. low frequency sound) and to accurately reproduce the sound we must only allow the low frequency signals to the woofers. 

To achieve this we can implement a band pass filter which only allows frequencies from 20 Hz to 3000 Hz and attenuates rest of the signal passing to woofers. Similarly for mid-range driver we can implement a band pass filter which only permits frequencies from 3000 Hz to 8000 Hz. 

A passive band pass filter designed by cascading a high pass filter with a low pass filter and has two cut-off frequencies. The band pass filter is a 2^nd order RC frequency filter.

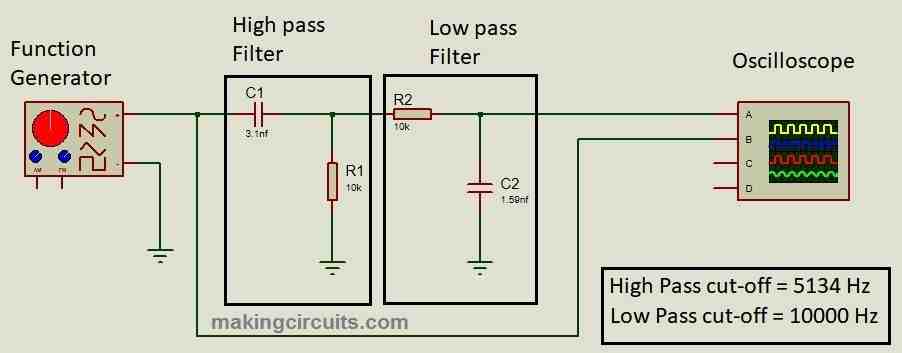
A band pass filter can be constructed successfully only if the high pass filter receives the input signal first as shown in the schematic and the cut-off frequency of low pass filter must be greater than high pass stage.

Assume the cut-off frequency of high pass filter is 5 KHz and cut-off frequency of low pass filter is 10 KHz, we can observe the following:

• If the input frequency is less than 5 KHz, the high pass filter will block the signals. Thus no or attenuated signal at the output. 
• If the input frequency is between 5 KHz and 10 KHz (say 7 KHz), the high pass filter will allow the signal to pass, since 7 KHz is higher than the cut-off frequency of HPF and the low pass filter (LPF) will also allow the signal to pass through, since the input is less than the cut-off frequency. Thus we will get signal at the output with little or no attenuation.   
• If the input frequency is greater than 10 KHz (say 15 KHz), the high pass filter will pass the signal, but since the input frequency has exceeded the cut-off frequency of low pass filter, it will attenuate the signal to a great extent. 
• In conclusion, we will get unaltered signal only with in the bandwidth of the filter.

How to calculate cut-off frequencies for band pass filter?

The cut-off frequency of low pass and high pass filter can be calculated by using the shown formula:

Fc = 1 / 2π x R x C

Where Fc is the cut-off frequency (-3 dB),

             R is value of resistor in ohm,

             C is value of capacitor in farad.

• For high pass filter:

Fc = 1 / 2π x 10000 x 3.1 x 10^-9

Fc = 5134.30 Hz

• For Low pass filter:

Fc = 1 / 2π x 10000 x 1.59 x 10^-9

Fc = 10009.74 Hz

• The bandwidth of the filter is:

Bw = 10009 Hz – 5134 Hz= 4875 Hz or (approx. 5 KHz)

• Center frequency or resonant frequency:

Resonant or center frequency is the point at which the gain of the output is at maximum (peak). The formula for resonant frequency is:

Fr = square root of (FL x FH)

Where, Fr is resonant frequency, FL is cut-off of LPF and FH is cut-off of HPF

Fr = square root of (10009 x 5134)

Fr = 7168 Hz, this is the frequency at which the output amplitude is at maximum.

Simulation for passive band pass filter:

At 600 Hz: At 600 Hz the output is heavily attenuated where in input frequency is below the 5 KHz.

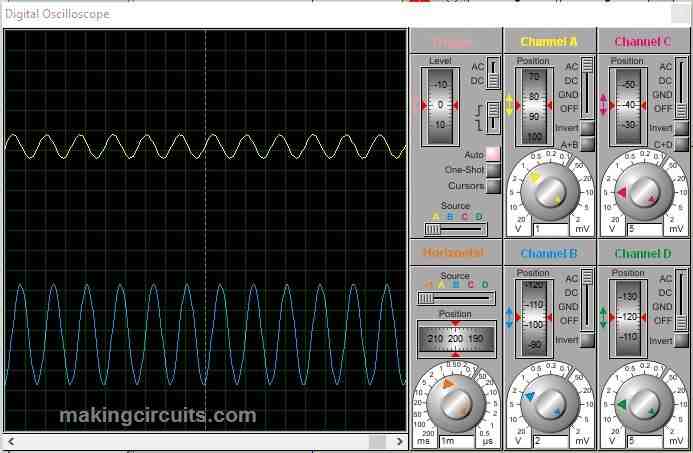
At 7 KHz: At 7 KHz the output is least attenuated and the input frequency is within the bandwidth of the filter circuit.  

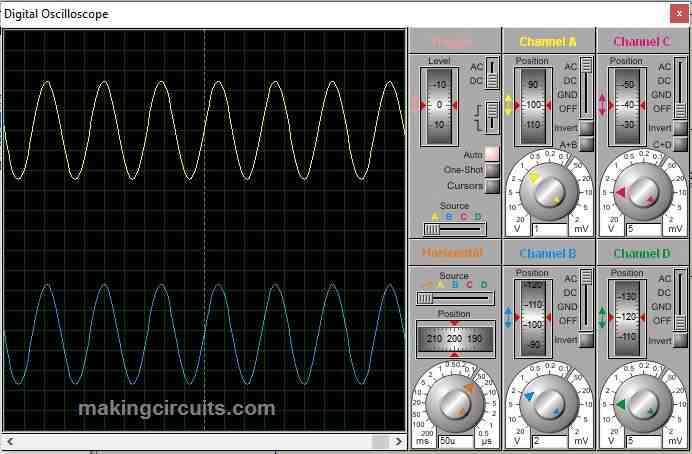
At 50 KHz: At 50 KHz input, the output got heavily attenuated. 

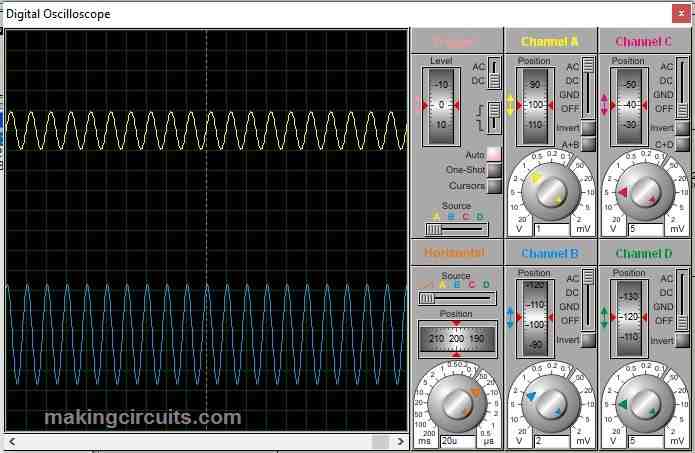
Frequency response graph of band pass filter:

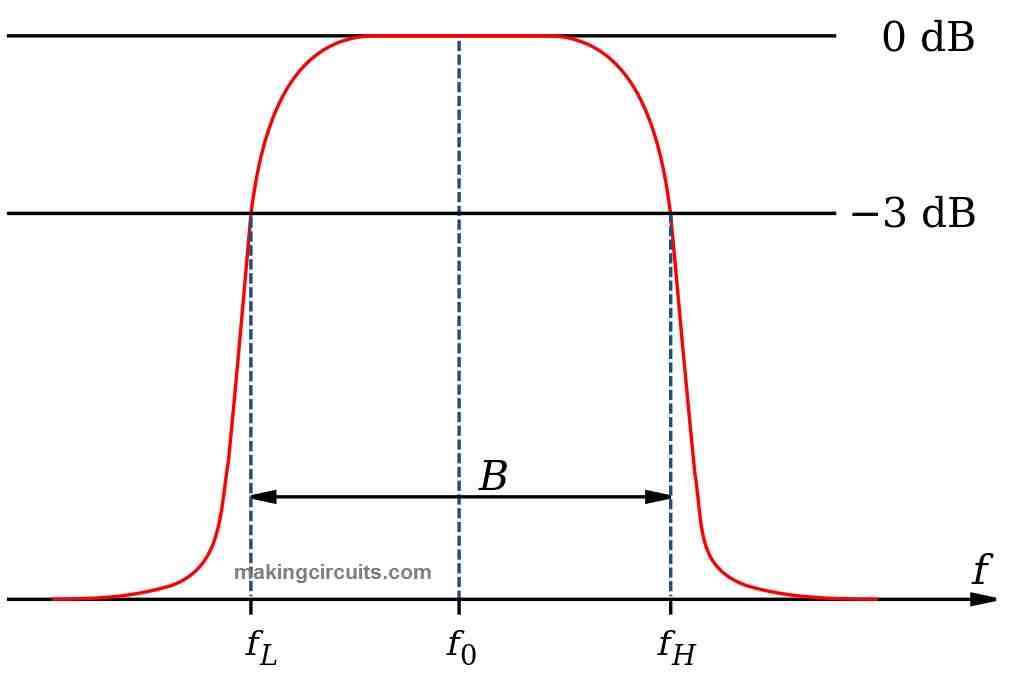
From the above frequency response graph we can infer that frequencies below FL and above FH are attenuated.

Active RC filters:

In this section we are going to explore about active RC filters. The main disadvantage of passive RC filter is the output getting attenuated since no amplification is involved and as we go for 2^nd order or higher order the output gets attenuated further.  

To overcome the disadvantage of RC passive filters, we are going to introduce an amplifier to the RC circuit, since an amplifier is an active component; hence we call them as active RC filters. 

The amplifiers that we can find in RC filters are generally op-amps, but we can also use BJT transistors, FETs etc. 

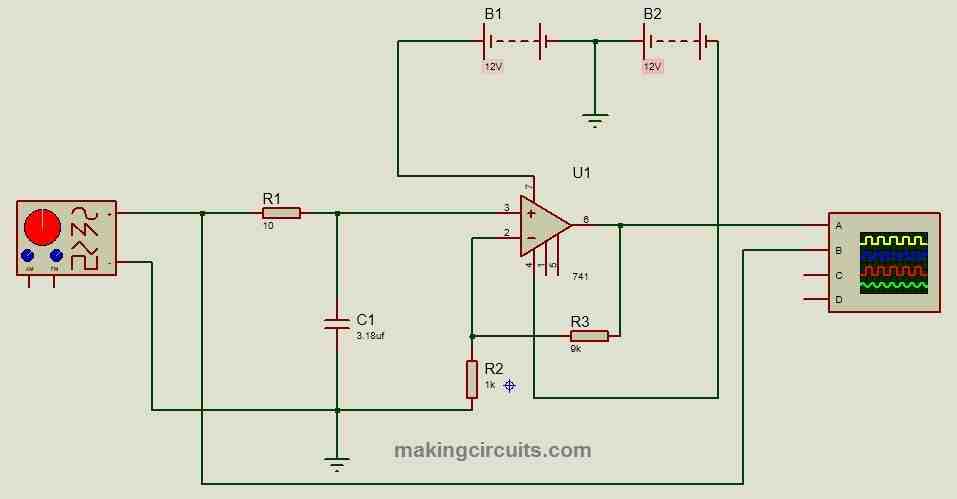
All the active RC filters we are going to illustrate have the following: IC 741, R3 = 9K, R2 = 1K for the gain. Dual 12V power supply with common ground is utilized, so that the output wave can go from +12V to -12V maximum, otherwise (with single supply) half of the wave will be chopped off at the output. 

The gain of the op-amp is fixed at 10 (no unit), meaning the output will be ten times higher than the input signal and the op-amp is configured as non-inverting amplifier.

Gain = 1 + (R3 / R2) = 1 + (9 / 1) = 10.

The frequency response, cut-off frequency and resonant frequency calculations etc. are exactly same as passive RC filters; the only difference here is we can control the gain / amplitude of output.

Active low pass filter:

Active high pass filter:

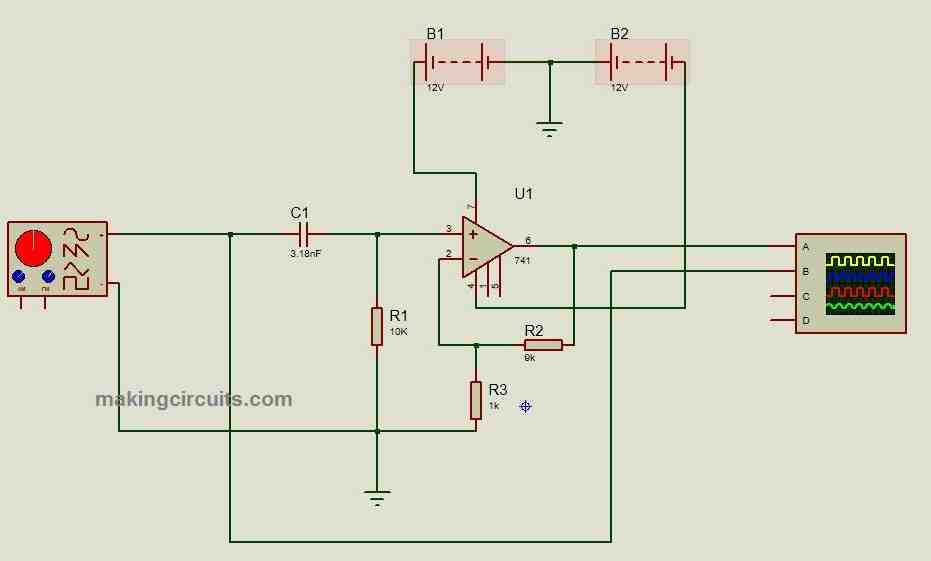
Active band pass filter:

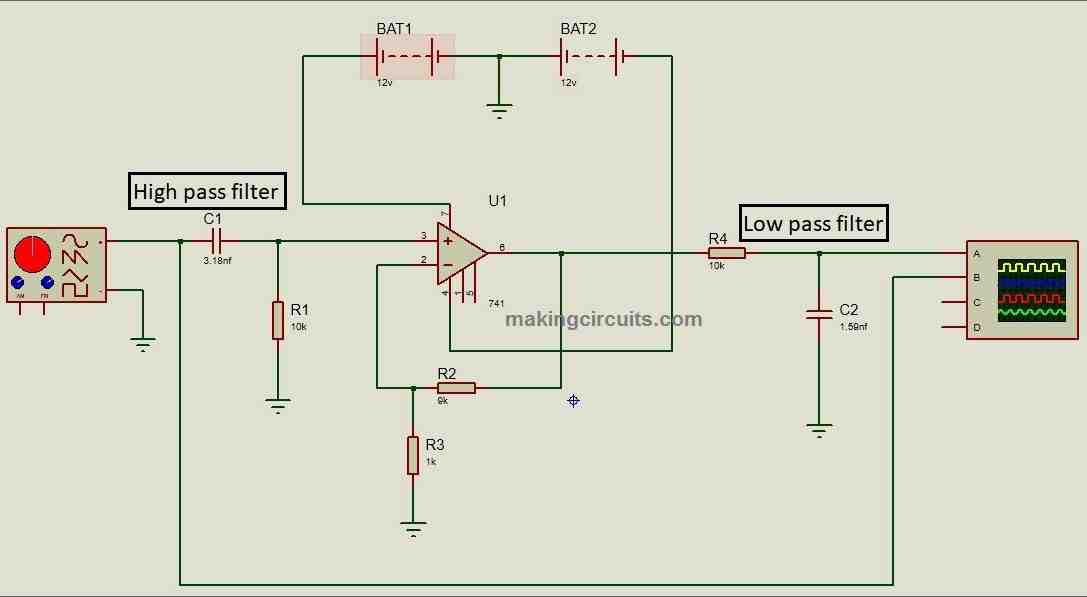
The outputs of above illustrated active RC filters are similar to of passive RC filters except the output amplitude will be larger than the input, you can see their outputs and also simulate on your PC / MAC, links given below. 

Please click the links below to download proteus simulation files:

• Passive low pass filter.
• Passive high pass filter.
• Passive band pass filter.
• Active low pass filter.
• Active high pass filter.
• Active band pass filter.