Resitivity which is also known as Coefficient of Resistance is a property in a substances which causes an opposition to current flow within that substance.
This can be easily calculated through formulas deduced from Laws of Resistance
Laws of Resistance
The amount of resistance in any material will depend on the following aspects: 1) The length of the material 2) Its Cross sectional Area 3) The natural properties of the material 4) The temperature of the material We have four important laws of resistance which can be used for calculating the resistivity or the specific resistance of any material.
First Law of Resistivity
According to the first law the resistance of any material is directly proportional to its length. Thus electrical resistance R of a material can be written as:
R ∝ L
where L is the length of the material.
Description: If the material length is longer, that will also increase the path through which the electrons have to travel across the material, This will force an increased number of collisions between the electrons, eventually reducing the number of electrons through the material. Due to the reduced electrons, ultimately the current across the material will also get reduced proportionately.
Put simply, as the length of a material increases, its resistance to current also increases linearly.
Second Law of Resistivity
The resistance of a material will be inversely proportional to its cross-sectional area. Electrical resistance R of any material is: R ∝ 1 / A
where A is the cross sectional area of the material.Description: The magnitude of current that can pass through a material is decided by the number of electrons travelling through the cross section of the material in one second. This implies that materials having larger cross sectional area will allow greater amount of electrons to pass through it, which would mean more current being allowed through the material. In this scenario, if the voltage remains fixed, higher rate of current would conversely mean lower electrical resistance, and this response will be perfectly linear.
Defining Resistivity
If we combine the above two expressions we get:

Where, ρ (rho) is the constant of proportionality called resistivity or specific resistance of the material or the conductor. Now suppose we replace, L = 1 and A = 1 in the above expression, it gives, R = ρ.
This signifies that resistance of a material having a unit length and unit cross - sectional area will be same as the values of its resistivity or specific resistance.
Thus in other words we can define Resistivity of a material as the electrical resistance across opposite a cubic section of the material having unit volume.

Third Law of Resistivity
The 3rd law states that the resistance of any material will be directly proportional to the resistivity of the content of the material.
All materials may differ with their magnitudes of resistvity.
Things like the number of free electrons, size of the atoms, the bonding property of the atoms, and many such aspects can determine the level of resistivity of a particular material.
A material having high resistivity will exhibit a higher level of resistance to current and vice versa, which will also a linear in nature.R ∝ ρ
Fourth Law of Resistivity
According to the fourth law, temperature plays a crucial role and can affect the resistance of a conductor seriously. This is due to the fact that heat energy has the ability to force an increased inter-atomic disturbance within a conductor, especially in metals. Because of this effect, electrons find excess obstacles on their way while traveling across the ends of the matter with a potential difference. Therefore, when metallic materials are subjected to higher temperatures, their resistance to electric current increases proportionately. Conversely, if the material is a non-conductor, increasing temperatures helps to reduce its overall resistance to current. This is because higher temperatures break the covalent bonds existing in non metallic materials enabling the release of free electrons, which quickly begin drifting in response to the applied potential difference. From the above descriptions we can understand that it can be illogical to specify the resistance of a conductor without considering the temperature around it.
Unit of Resistivity
The unit of resistivity could be quickly calculated by solving the following equation:
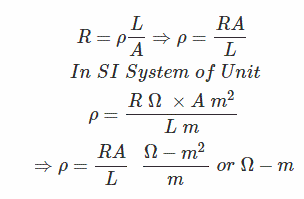
The unit of resistivity is measured in Ω - m in MKS system and Ω - cm in CGS system and 1 Ω - m = 100 Ω - cm.
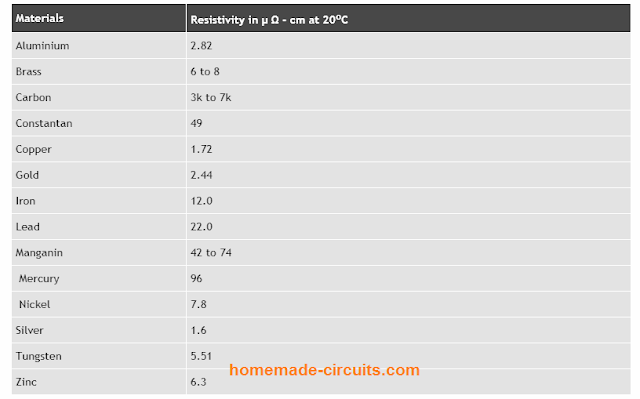
Complete List showing the Resistivity of a variety of matters commonly used in everyday applications
Variation of Resistance with Temperature
There are a number of substances primarily metallic items, like silver, copper, aluminum, which possess an abundance of free electrons. Consequently such type of substances are able to conduct current without difficulty, in other words they they turn less resistive to electric current.
However the resistivity of such elements is hugely vulnerable to temperature differences. Typically metals present an increased electrical resistance when temperature on them is increased. Conversely the resistance exhibited by a nonmetallic element typically lowers in response to increased temperatures. Let's consider the example of a portion of pure metal and subject it to 0 degree Celsius temperature using ice, and subsequently let's increase its temperature progressively from 0℃ to to 100℃ by applying an external heat source. While the temperature is increased if its resistance is measured at frequent intervals, we would realize that electrical resistance of the metallic element steadily increases as temperature increases.
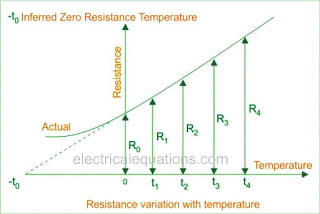
Plotting a graph of the change in the resistance of the metal against temperature i.e. resistance Vs temperature, we could obtain a straight line as indicated in the image shown below. If we extend this straight line across the resistance axis, we will find that it cuts the temperature axis at certain temperature = - t0℃.
This clearly indicates that at this temperature the metal attains an electrical resistance equal to zero.
This temperature is called "inferred zero resistance temperature".
Although hypothetically this is proven, zero resistance is never feasible for any material in this practical world.
In fact rate at which the resistance of a material varies in response to temperature changes is never constant throughout the stipulated range of temperature.
We can also find the precise graph in the figure below.
If we imagine R1 and R2 as the measured resistances for the temperatures t1℃ and t2℃ respectively. Then we can easily present the equation as expressed below,
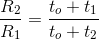
The above formula helps us to calculate the resistance of a given metal at various temperature levels. Let's say we have a known resistance value R1 for a metal at a temperature level of t1℃, so now in we have the inferred zero resistance temperature value t0 with us, will quickly enable us to evaluate the unknown resistance value R2 for any level of temperature t2℃ by using the aforementioned formula.
The above discussed property is fundamentally used for evaluating a possible variation in the resistance of an electrical machine due to a change of temperature on it.
For example, the formula above is applied for determining the amount of resistance that may increase in a transformer due to the rise in temperature of its winding. This could be otherwise impossible to achieve since the internal sections of the transformer is simply inaccessible to us, but fortunately the resistance variation due to heat phenomenon, allows us to calculate this quite easily through formulas and graphical assistance.
Once the resistance to electricity of the transformer winding is identified throughout its initial stage until the finish stage of the test run, we are able to calculate and acquire an estimation regarding the rate of increase of temperature of its winding during its practical operational periods.
Normally a reference value of 20℃ is considered as the standard reference whenever the resistance of a device or component is specified. For example, when we talk about say a 20 Ohm resistor it signifies that the resistance will have this value at 20℃ ambient temperature, and may begin varying (increasing) its resistance proportionately as the temperature rises above this value.

Leave a Reply