AC Waveform and AC Circuit Theory

AC Sinusoidal Waveforms can be produced by simply spinning a coil or an inductor close to a magnetic field and the generated switching voltages and currents become the foundation of AC Principle

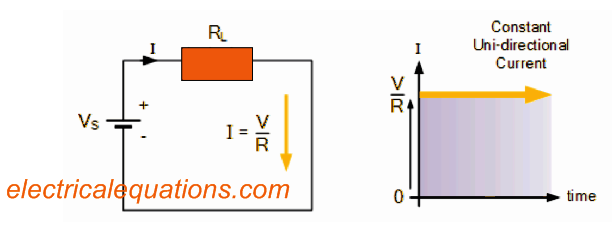
Direct Current or D.C. as it is more typically called, is a kind of electrical current or voltage that runs through an electrical network in a single path only, rendering it a “Uni-directional” supply.

Typically, the two DC currents and voltages are generated by batteries, power supplies, solar panels, dynamos and solar cells among other things.

A DC voltage or current carries a predetermined value (amplitude) and a precise flowing path.

For instance, +12V signifies 12 volts through the positive path, similarly -5V signifies 5 volts towards the negative direction.

We likewise understand that DC power supplies never alter their magnitudes in relation to time, these are a persistent value moving with a constant stable direction.

Meaning, DC preserves identical value all the time, and its continuous uni-directional DC supply never shifts or turns negative except when the supply polarities are literally changed.

A good example of a basic DC or direct current circuit is proven below.

An alternating function or AC Waveform in contrast is described as current that changes with both dimensions and direction approximate uniformity with regard to time turning it into a “Bi-directional” waveform.

An AC function could symbolize either a source of power or a signal having the structure of an AC waveform.

It will typically follow a mathematical sinusoid represented as:

A(t) = Amax*sin(2πƒt).

The phrase AC or Alternating Current, commonly describes a waveform varying with time, and is better recognized as a Sinusoidal Waveform.

Sinusoidal waveforms are more commonly identified by their small phrase Sine Waves.

Sine waves are definitely the most crucial forms of AC waveform employed in electrical engineering.

The shape acquired by tracing the instantaneous ordinate principles of voltage or current with respect to time is known as an AC Waveform.

An AC waveform will be seen continuously modifying its polarity every single half cycle, switching across a positive optimum level and a negative optimum level correspondingly with respect to time.

A popular illustration of AC is our household mains voltage supply.

What this means is AC Waveform is actually a “time-dependent signal”. The most common type being the Periodic Waveform.

The periodic or AC waveform is the result of a revolving alternator.

Typically, the shape of any kind of periodic waveform could be developed through a fundamental frequency and superimposing it along with harmonic signals of varying amplitudes and frequencies.

It is not possible to save or store Alternating voltages and currents in batteries or cells as may be done with direct current (DC).

But it is less of a challenge and less expensive to generate AC through alternators or function generators whenever needed.

The dimensions of an AC waveform are determined by the generator producing it.

However, most AC waveforms incorporate a zero voltage central line that will split the waveform into a pair of symmetrical halves.

The primary characteristics of an AC Waveform can be defined as:

AC Waveform Characteristics

The Period, (T) is the time length in seconds taken by the waveform to repeat its cycles from beginning to end. This could likewise be named the Periodic Time for sine waves, or the Pulse Width for square waves.
The Frequency, (ƒ) is determined by the number of times the waveform cycle repeats in a single second time frame. Frequency may be the reciprocal of the time period, ( ƒ = 1/T ). The unit of frequency is measured in Hertz, (Hz).
The Amplitude (A) is the magnitude or the value of the waveform measured in volts and/or amperes.

Typically, for AC waveforms the horizontal central line symbolizes a zero base for either voltage or current.

Any portion of an AC showing up over the horizontal zero axis signifies a voltage or current moving in a single path.

In the same way, any section of the waveform presenting itself below the horizontal base indicates a voltage or current streaming in the reverse path in comparison to the previous counterpart.

Usually for sinusoidal AC waveforms the path of the wave cycle reaching above the zero base will be equivalent to the path formation beneath it.

Having said that, for the majority of non-power AC signals like audio waveforms this is simply may not be always true.

The commonest periodic signal waveforms applied in Electrical, Electronic Engineering are the Sinusoidal Waveforms.

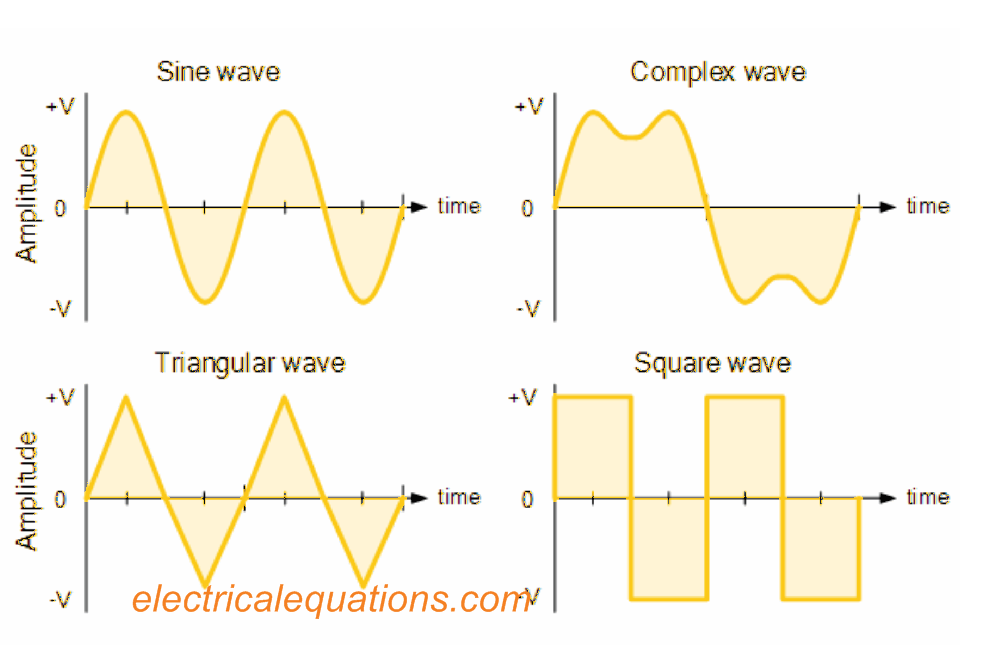
On the other hand, an AC waveform might not continually acquire a smooth appearance centered about the trigonometric sine or cosine function.

AC waveforms may sometimes acquire the shape of Complex Waves, Square Waves or Triangle Waves, all these can be visualized below:

The time required for an AC Waveform to accomplish a single complete routine, starting from its positive half to its negative half and back to its zero base again is known as a Cycle.

Thus, one full AC cycle includes both a positive half-cycle and a negative half-cycle.

The time utilized to finish one complete cycle is known as the Periodic Time of the waveform, and is presented by the symbol “T”.

The number of full cycles generated per second (cycles/second) known as the Frequency.

It is denoted as ƒ which symbolizes frequency of the alternating waveform. Frequency is measured in Hertz, ( Hz ) titled after the German physicist Heinrich Hertz.

We can also see an association between cycles (oscillations), periodic time and frequency (cycles per second), therefore when there are ƒ number of cycles per second, every unique cycle will require 1/ƒ seconds for the completion.

Relationship Between Frequency and Periodic Time

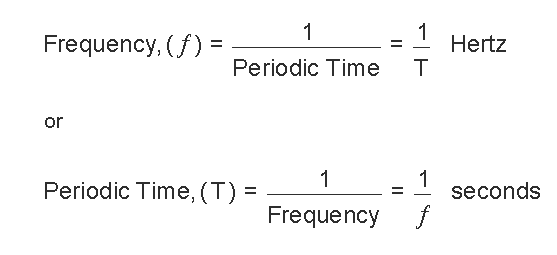
AC Waveform Example No1

Show the periodic time, having a 50Hz waveform and
2. Provide the frequency of an AC waveform having a periodic time of 10mS.

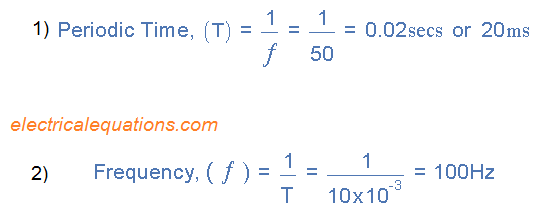
Frequency was previously stated in “cycles per second” abbreviated as “cps”, currently it is more typically described in units named “Hertz”.

For any home-based mains supply the frequency is going to be often 50Hz or 60Hz dependent on the country and is established by the rotational speed of the hydro generator.

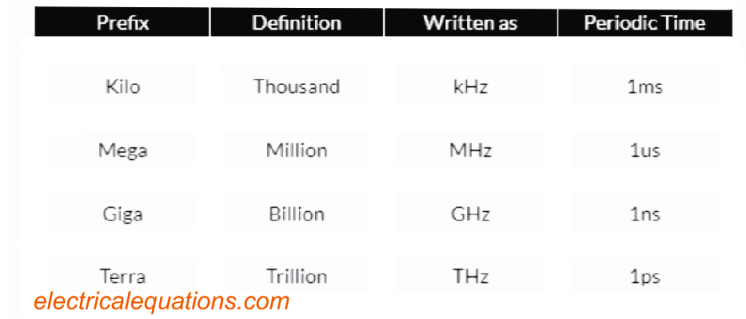
Yet one hertz looks a very tiny unit, therefore prefixes are employed that represent the sequence of values of the waveform at larger frequencies, for instance kHz, MHz as well as GHz.

Frequency Prefix Definitions

AC Waveform Amplitude

In addition to knowing the periodic time or the frequency of the AC, there’s yet another essential parameter of the AC waveform named Amplitude. It’s also called the Maximum or Peak value, and symbolized by the phrases, Vmax for voltage or Imax for current.

The peak value is the biggest level or point of the voltage or current where the waveform is able to extend to, in yhe course of its every half cycle, measured from the zero axis.

In contrast to a DC voltage that carries a constant level which could be evaluated through Ohm’s Law, a switching AC will be continually altering its value with respect to time..

This peak value for pure sinusoidal waveforms will be identical at all times for both half cycles ( +Vm = -Vm ).

However for non-sinusoidal or intricate waveforms the peak value is often very diverse for each half cycle.

Occasionally, alternating waveforms have a peak-to-peak, Vp-p value which denotes the distance or the total of voltage between the optimum peak value, +Vmax and the lowest peak value, -Vmax in the course of each full cycle.

AC Waveform Average Value

The average value of DC voltage will invariably identical to its highest peak value. This is because a DC voltage is constant.

This average DC value is only going to change only its duty cycle changes. For a pure sine wave if the average value (actually called the mean value) is tested within the full cycle, would be equal to zero.

This is because the positive and negative halves have the tendency of cancelling one another away.

Therefore the mean value of an AC waveform will be determined or tested across its half cycle only as depicted below.

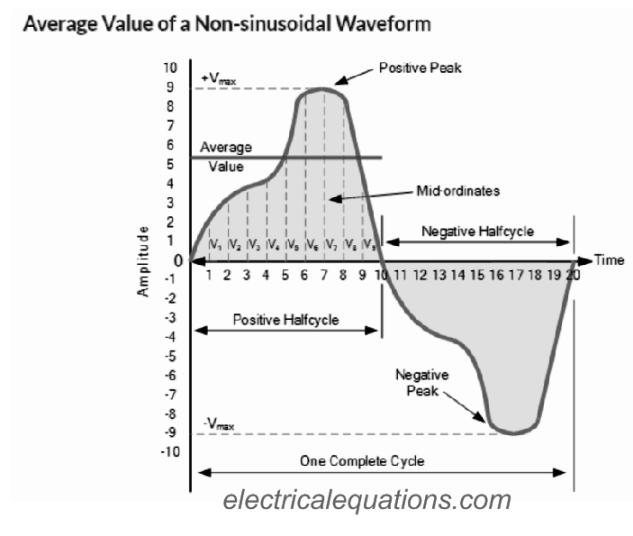
Average Value of a Non-sinusoidal Waveform

To obtain the mean value of a waveform cycle we have to determine the region lying below it by applying the mid-ordinate rule, trapezoidal rule or the Simpson’s rule, commonly used in mathematics.

The approximate region below any unpredictable waveform can be quickly identified by implementing the mid-ordinate rule.

To obtain the mean value of a waveform cycle we have to determine the region lying below it by applying the mid-ordinate rule, trapezoidal rule or the Simpson’s rule, commonly used in mathematics.

The approximate region below any unpredictable waveform can be quickly identified by implementing the mid-ordinate rule.

The zero base line can be split into many equivalent sections. In our illustration above this estimate ended up being 9, ( V1 to V9 ).

The greater ordinate lines the greater will be the accuracy of the mean value.

This will be the sum of all the instantaneous values added collectively and then divided by the total number.

This can be presented as.

Average Value of an AC Waveform

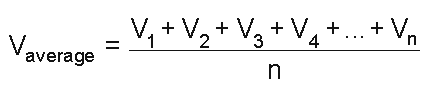
Where: n signifies the exact quantity of mid-ordinates applied.

For any pure sinusoidal waveform this mean value will invariably be equivalent to 0.637*Vmax. This specific relationship furthermore is valid for average current values.

The RMS Value of an AC Waveform

The mean value of an AC worked out above at: 0.637*Vmax is NOT the same value that may be measured for a DC supply.

The reason being as opposed to a DC supply which can be constant with a fixed value, an AC waveform is periodically modifying its rate of movement, and possesses no permanent value.

Hence comparable value for an alternating current system delivering the identical level of electrical power to a load as a DC counterpart is actually referred to as “effective value”.

The effective value of a sine wave delivers exactly the same I2*R heating dissipation output to a connected load as from a constant DC supply.

It is more typically referred to as the Root Mean Squared or simply RMS value.

It is measured as the square root of the mean of the square of the voltage or current.

That is Vrms or Irms is presented as the square root of the average of the sum of all the squared mid-ordinate values of the sine wave.

The RMS value for just about any AC waveform can be determined by implementing the below shown modified average value formula

RMS Value of an AC Waveform

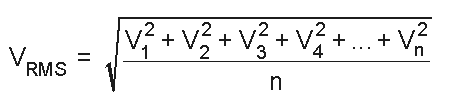
Where: n is the quantity of mid-ordinates.

This effective or R.M.S. value will invariably be also the same as: 1/√2Vmax that is equal to 0.707Vmax

This relationship is valid for RMS current values. The RMS value for a sine waveform will be always higher than the average value excluding a rectangular waveform.

In such cases the heating result continues to be stable hence the average and the RMS values would be the identical.

One important opinion about R.M.S. values is that the majority of multimeters, both digital and analogue unless specified only assess the R.M.S. values of voltage and current which may not be the average.

For that reason while testing a DC with a a multimeter the result on the meter is going to be corresponding to I = V/R. For an AC system the reading is going to be equivalent to Irms = Vrms/R.

Furthermore, apart from average power calculations, in case of RMS or peak voltages, make sure to use VRMS to obtain IRMS values, or peak voltage, Vp to find peak current, Ip values.

Please never confuse them together because Average, RMS or Peak values of a sine wave will be entirely different and your evaluations will certainly be erroneous.

Form Factor and Crest Factor

Despite the fact that this is not often used today, both Form Factor and Crest Factor enable you to provide details regarding the genuine shape of the AC waveform.

Form Factor is actually the ratio between the average value and the RMS value. It is represented as:

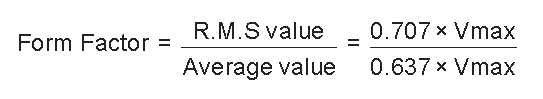
When a pure sinusoidal waveform is involved the Form Factor becomes equal to 1.11. Crest Factor is the ratio between the R.M.S. value and the Peak value of the AC. It is evaluated with the following formula:

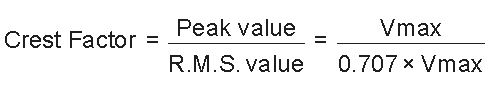
For a pure sinewave the Crest Factor can be found equal to 1.414.

AC Waveform Example No2

An AC sinewave having 6 amps current when applied over 40Ω resistor, calculate the average and the peak voltage of the supply.

The R.M.S. Voltage value is evaluated as shown here:

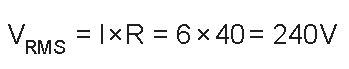
For calculating Average Voltage the following formula could be used

Nest, the Peak Voltage value may be calculated as:

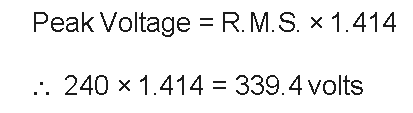
The calculation and implementation of Average, R.M.S, Form factor and Crest Factor could be for all forms of periodic waveform.

These may include Triangular, Square, Sawtoothed or any type of unpredictable or intricate voltage/current pattern.

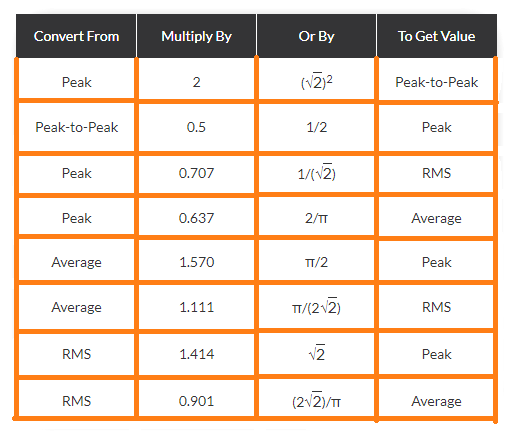
Conversion process across the different sinewave values can often be complicated.

For this reason the below shown table provides a hassle-free technique of switching one sine wave value to a new one.

Sinusoidal Waveform Conversion Table

In the next our upcoming tutorial we are going to glance at the fundamentals of producing a sinusoidal AC waveform (a sinusoid) and angular velocity representation.