From our earlier discussions we have understood that electrical resistance of all elements changes in response to the variations in its temperature.
Temperature coefficient of resistance is defined as the magnitude by which the electrical resistance of a material changes in response to each degree change of temperature.
If we consider a conductor with a resistance value of R0 at 0oC and Rt at toC correspondingly.
By applying the equation of resistance variation with temperature we obtain

The term αo is called temperature coefficient of resistance of that substance at 0oC temperature.
From the above equation we can understand that temperature affects the electrical resistance of a body basically depending on the following three aspects:
- the body's resistance at initial temperature,
- the rate temperature rise and
- the temperature coefficient of resistance αo.
The value of αo may vary for different materials, therefore resulting change in resistance due to temperature may not be equal and may show variations accordingly.
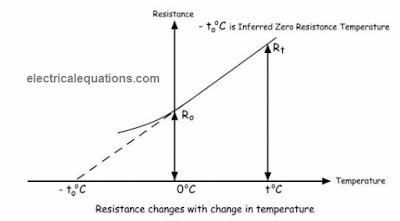
This implies that the temperature coefficient of resistance of a material at 0 degrees Celsius will be the reciprocal of its inferred zero resistance.
From our earlier discussions we learned that in metallic substances the resistance increases with increase in temperature, however there also exists materials that show an opposite behavior, meaning in such materials resistance decreases when their temperature increases.
In metals an increase in temperature forces a disturbance in the normal motion of the free electrons leading to an increased interatomic vibration, which in turn leads to higher collision across the electrons.
This disturbance hampers the gentle movement of the electrons causing an increased resistance to the free flow electrons. Due to this we find the coefficient of resistance for metals is always positive.
However when we consider semiconductors or other nonmetal variants, we see that the quantity of free electrons in them rises with rise in their temperature.
Due to the fact that increased temperature deliver ample warmth to the atomic crystal, a substantial amount of covalent bonds begin breaking up, and therefore more free electrons are generated.
Meaning when these materials are subjected to higher temperatures, a large amount of electrons in them acquire sufficient energy to free themselves from the valence orbits and penetrate through the conduction bands, by traversing the forbidden energy gap.
With an increase in the number of free electrons, the resistance of these nonmetallic material decreases with a rise in temperature.
Therefore temperature coefficient of resistance is negative for nonmetallic materials and semiconductors. If the change in resistance with temperature is negligible, we could the coefficient of temperature could be considered to be zero.
The alloy of constantan and manganin are regarded as materials having temperature coefficient of resistance close to zero. The value of this coefficient may not be constant, this will depend on the starting temperature point from where the rise in temperature began.
When this gradual rise starts from an initial temperature of 0℃, the value of this coefficient is αo, which is basically the reciprocal of the specific inferred zero resistance temperature of the material.
However for other initial temperature values, the temperature coefficient of electrical resistance could be different from αo. To be precise, for almost any substance, the magnitude of this coefficient will be highest at 0℃ temperature.
For example, assuming the value of this coefficient of a given substance at a given t℃ is αt, then its value could be identified through the below shown equation,

In the above expression, the coefficient value at a t2oC temperature for an identical t1oC temperature can be written as,
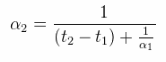
Reassessing the Theory of Temperature Coefficient of Resistance
The electrical resistance of conductors for example silver, copper, gold, aluminum, etc., is determined by collisions happening between electrons inside the substance.
With an increase in temperature, the collision across the electrons collision become quicker, resulting in a greater resistance level of the conductor.
The resistance of conductors typically increase as their body temperature is increased. If we consider a conductor having a resistance value R1 at t1oC, let's imagine due to a rise in temperature, its resistance leevates to a avalue R2 at t2oC. Then this increase in resistance (R2 - R1) due to the rise in temperature (t2 - t1) will depend on following factors:
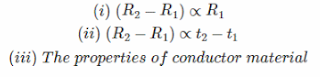
Combining the above expressions helps us to derive the following equations:

Where, α is the temperature coefficient of resistance of material at t1oC. Rearranging the terms in Equation (1) gives us the following:

For a specific temperature, if the resistance and temperature coefficient of resistance of material are known, then we are able to calculate the resistance of substance at other ranges of temperatures by applying equation (2).
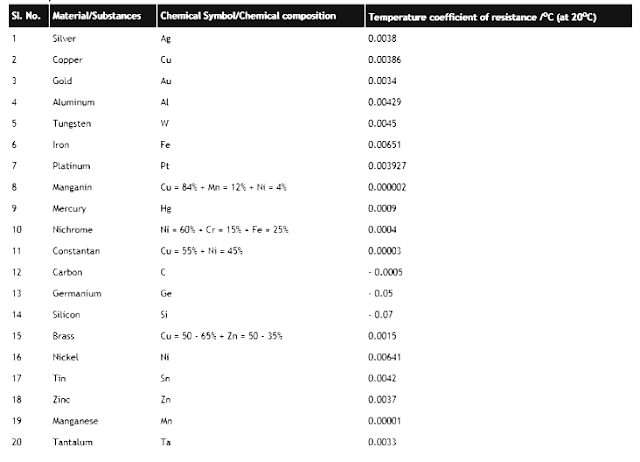
List of Temperature Coefficient of Resistance of assorted Materials
The temperature coefficient of resistance of a few assorted materials and substances at 20oC are shown in the following table-
Influence of Temperature on Temperature Coefficient of Resistance of a Substance
We have understood that temperature is also responsible for changing the temperature coefficient of resistance of a substance.
Assuming αo as the temperature coefficient of resistance of material at 0oC, then evaluating equation (2), we find the resistance of material at toC to be,
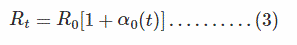
Where, R0 is recognized as the Resistance of material at 0oC
Similarly, when a material has a temperature coefficient of resistance αt, at toC, then from equation (2) the resistance of the material at 0oC is evaluated as:
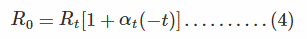

Where, α1 and α2 form the temperature coefficient of resistance of the substance at t1oC and t2oC correspondingly.
Therefore, when we are aware of the temperature coefficient of resistance of a given substance at a specific temperature, we can quickly determine the temperature coefficient of material at some other temperature by applying equation (6).
Good conductors of heat and electricity carry larger positive temperature coefficient of resistance.
As a result, the resistance of conductors such as metals increases with increasing temperature levels.
Semiconductors and insulating material on the other hand that possess negative temperature coefficient of resistance reveal a decreasing resistance level in response to rising temperature levels. Alloys, for example manganin, constantan, etc. have characteristics of very low and positive temperature coefficient of resistance.
Consequently, the resistance of alloys increases with increasing temperature levels however this increase in resistance is rather sluggish (practically minimal) when compared with various other metals that are used for making these alloys and suited for implementing in measuring tools.
Leave a Reply